Tree dan Graff

1 Algoritma Djikstra

A.    Definisi Algoritma Djikstra

Algoritma Dijkstra, (penemunya adalah seorang ilmuwan komputer, Edsger Dijkstra), adalah sebuah algoritma yang dipakai dalam memecahkan permasalahan jarak terpendek untuk sebuah graph berarah dengan bobot-bobot sisi yang bernilai positif.

B.     Tujuan Algoritma Dijkstra

1.    Tujuan Algoritma Dijkstra yaitu untuk menemukan jalur terpendek berdasarkan bobot terkecil dari satu titik ke titik lainnya.

2.    Kelemahan algoritma ini adalah semakin banyak titik akan semakin memakan waktu proses.

3.    Jumlah titik menentukan tingkat efektifitas dari algoritma djikstra.

C.    Urutan Logika Algoritma Dijkstra

1.    Beri nilai bobot (jarak) untuk setiap titik ke titik lainnya, lalu set nilai 0 pada node awal dan nilai tak hingga terhadap node lain (yang belum terisi).

2.    Set semua node “Belum terjamah” dan set node awal sebagai “Node keberangkatan”.

3.    Dari node keberangkatan, pertimbangkan node tetangga yang belum terjamah dan hitung jaraknya dari titik keberangkatan.

4.    Setelah selesai mempertimbangkan setiap jarak terhadap node tetangga, tandai node yang telah terjamah sebagai “Node terjamah”. Node terjamah tidak akan pernah di cek kembali, jarak yang disimpan adalah jarak terakhir dan yang paling minimal bobotnya.

5.    Set “Node belum terjamah” dengan jarak terkecil (dari node keberangkatan) sebagai “Node Keberangkatan” selanjutnya dan lanjutkan dengan kembali ke step 3.

Contoh :

Titik mengambarkan lokasi dan garis menggambarkan jalan, maka algoritma Dijkstra melakukan kalkulasi terhadap semua kemungkinan bobot terkecil dari setiap titik.

Pertama tentukan titik yang akan menjadi nomor kode (node) awal, lalu beri bobot jarak pada node pertama ke node terdekat satu per satu, lalu akan dilakukan pengembangan pencarian dari satu titik ke titik selanjutnya (tahap demi tahap).

1.    Node awal 1, Node tujuan 5. Setiap edge yang terhubung antar node telah diberi nilai.
                     

2.    Dijkstra melakukan kalkulasi terhadap node tetangga yang terhubung langsung dengan node keberangkatan (node 1), dan hasil yang didapat adalah node 2 karena bobot nilai node 2 paling kecil dibandingkan nilai pada node lain, nilai = 7 (0+7).

3.    Node 2 diset menjadi node keberangkatan dan ditandai sebagi node yang telah terdatangi. Dijkstra melakukan kalkulasi kembali terhadap nodenode tetangga yang terhubung langsung dengan node yang telah terdatangi. Dan kalkulasi dijkstra menunjukan bahwa node 3 yang menjadi node keberangkatan selanjutnya karena bobotnya yang paling kecil dari hasil kalkulasi terakhir, nilai 9 (0+9).

                           

4.    Perhitungan berlanjut dengan node 3 ditandai menjadi node yang telah terjamah. Dari semua node tetangga belum terjamah yang terhubung langsung dengan node terjamah, node selanjutnya yang ditandai menjadi node terjamah adalah node 6 karena nilai bobot yang terkecil, nilai 11 (9+2).

5.    Node 6 menjadi node terjamah, dijkstra melakukan kalkulasi kembali, dan menemukan bahwa node 5 (node tujuan ) telah tercapai lewat node 6. Jalur terpendeknya adalah 1-3-6-5, dan niilai bobot yang didapat adalah 20 (11+9). Bila node tujuan telah tercapai maka kalkulasi dijkstra dinyatakan selesai.

2.2 Algoritma Kruskal

A. Definisi Algoritma Kruskal

Algoritma kruskal adalah sebuah algoritma dalam teori graf yang mencari sebuah minimum spanning tree untuk sebuah graf berbobot yang terhubung. Ini berarti menemukan subset dari tepi yang membentuk sebuah pohon yang mencakup setiap titik , di mana berat total dari semua tepi di atas pohon diminimalkan.. Jika grafik tidak terhubung, maka menemukan hutan rentang minimum (pohon rentang minimum untuk setiap komponen terhubung). Algoritma Kruskal juga tergolong algoritma Greedy dalam teori graf yang digunakan untuk mencari minimum spanning tree. Algoritma ini pertama kali muncul pada tahun 1956 dalam sebuah tulisan yang ditulis oleh Joseph Kruskal. Algoritma Kruskal adalah contoh dari algoritma rakus. Algoritma ini pertama kali muncul dalam Prosiding American Mathematical Society, hal 1956.

Dasar pembentukan algoritma Kruskal berasal dari analogi growing forest. Growing forest maksudnya adalah untuk membentuk pohon merentang minimum T dari graf G adalah dengan cara mengambil satu per satu sisi dari graf G dan memasukkannya ke dalam pohon yang telah terbentuk sebelumnya. Seiring dengan berjalannya iterasi untuk setiap sisi, maka forest akan memiliki pohon yang semakin sedikit. Oleh sebab itu, maka analogi ini disebut dengan growing forest. Algoritma Kruskal akan terus menambahkan sisi – sisi ke dalam hutan yang sesuai hingga akhirnya tidak akan ada lagi forest dengan, melainkan hanyalah sebuah pohon yang merentang minimum.

Graph : kumpulan dua himpunan yaitu himpunan titik ( vertex / simpul / node ) dan kumpulan dari garis ( edge ).

Tree : graph tak berarah yang terhubung dan tidak mengandung sirkuit. 

Sirkuit : simpul awal = simpul akhir.

Secara umum  Algoritma Kruskal ditulis :

1.    T masih kosong .

2.    pilih sisi (i,j) dengan bobot minimum.

3.    pilih sisi (i,j) dengan bobot minimum berikutnya yang tidak membentuk cycle di T, tambahkan (i,j) ke T.

4.    Ulangi langkah 3 sebanyak (n-2) kali.

5.    Total langkah (n-1) kali

B.     Karakteristik Algoritma Kruskal Sifat Algoritma Kruskal ini:

1.    Ia bekerja tidak hanya dengan grafik diarahkan.

2.    Ia bekerja dengan bobot dan tidak grafik tertimbang. Tapi, yang lebih menarik, apabila tepi yang berbobot.

3.    Kruskal adalah jenis algoritma serakah yang menghasilkan solusi optimal MST.

 

Langkah Algoritma Kruskal

Langkah-langkah utama Algoritma Kruskal adalah sebagai berikut:

1.    Atur tepi berat: paling berat pertama dan terberat terakhir.

2.    Pilih yang paling ringan tidak diperiksa tepi dari diagram.

3.    Tambahkan tepi memilih ini ke pohon, hanya jika hal itu tidak akan membuat siklus.

Menghentikan proses kapanpun n – 1 tepi telah ditambahkan ke pohon.

C.    Kelebihan dan Kekurangan Algoritma Kruskal

Terdapat dua macam algoritma tipe greedy yang dapat memenuhi pemecahan masalah pohon merentang ini. Yaitu algoritma Prim dan algoritma kruskal, berikut adalah kelebihan dan kekurangan algoritma Kruskal dibanding algoritma prim. a. Kelebihan Algoritma Kruskal

Kelebihan algoritma Kruskal dibanding algoritma prim adalah sebagai berikut :

Sangat cocok diterapkan saat graf memiliki sisi berjumlah sedikit namun memiliki sangat banyak simpul, karena orientasi kerja algoritma ini adalah berdasarkan pada urutan bobot sisi, tidak berdasarkan simpul.

b. Kekurangan Algoritma Kruskal

Beberapa hal yang menjadi kekurangan algoritma kruskal dibanding algoritma prim:

Kurang cocok digunakan saat graf lengkap atau yang mendekati lengkap, dimana setiap simpul terhubungkan dengan semua simpul yang lain. Karena algoritma Kruskal menitik beratkan pada pencarian sisi, dimana sisi-sisi tersebut harus diurutkan dan ini memakan waktu yang tidak sedikit

D.    Contoh Penyelesaian dengan Algoritma Kruskal

Contoh penyelesaian kasus minimun spanning tree dengan algoritma kruskal, diketahui sebuah graf berbobot seperti gambar 2.10 dibawah ini

Tabel 2. 1 Daftar urut nilai Graf dari sisi terbesar sampai terkecil

Bobot	Ruas
15	D,E
9	B,D	E,F
8	B,C	B,E	F,G
7	A,D	C,E
6	A,B	E,G
5	D,F

Penyelesaian:

1.    Mula-mula kita buat sekumpulan titik G hanya terdiri dari simpulsimpul saja.

2.    Urutkan Ruas dari bobot kecil ke besar (DF, AB, EG, AD, CE, BC, BE, FG, BD, EF, DE), kemudian berdasarkan urutan tersebut, kita menambahkan ruas dengan mencegah terbentuknya sirkuit.

Gambar 2. 1 Teknik penyelesaian Spanning Tree dengan Metode Kruskal

Spanning Tree adalah sebagai berikut :

a.    Pilih ruas terkecil dari keseluruhan graf secara acak. Ruas DF adalah ruas terkecil dengan bobot 5 (gambar 2.11 (a))

b.    Setelah ruas 1 didapatkan, ulangi lagi pemilihan ruas terkecil secara acak dari keseluruhan graf. Ruas AB dan ruas EG adalah ruas terkecil dengan bobot 6. Pilih acak ruas AB (Gambar 2.11(b))

c.    Lanjutkan untuk ruas yang selanjutnya, Ruas EG adalah ruas terkecil dengan bobot 6 dan tidak membentuk sirkuit jika dihubungkan. Maka pilih ruas EG

(Gambar 2.11(c))

d.   Pilih ruas selanjutnya dengan bobot yg terkecil saat ini, yaitu ruas AD dan ruas CE dengan bobot 7. Pilih acak ruas AD (Gambar 2.11(d))

e.    Lanjutkan untuk ruas CE adalah ruas terkecil dengan 7 dan tidak membentuk sirkuit jika dihubungkan. Maka pilih ruas CE (Gambar 2.11(e))

f.     Ruas selanjutnya dengan bobot yg terkecil saat ini yaitu ruas BC, BE dan FG dengan bobot 8. Pilih acak ruas BC dan hapus ruas BE (Gambar 2.11(f)) dan ruas FG karena akan membentuk sirkuit jika dihubungkan (Gambar

2.11(g))

g.    Untuk ruas-ruas selanjutnya, BD, EF,dan DE dihapus karena akan membentuk sirkut jika dihubungkan (Gambar 2.11(h), Gambar 2.11(i),

Gambar 2.11(j))

h.    Gambar 2.11(k) adalah Minimum Spanning Tree yang dihasilkan.

2.3 Contoh Listing Program

B. Algoritma Kruskal

2.4 Hasil Running

   B. Algoritma Djiktra

B. Algoritma Kruskal

               

KASUS ALGORITMA KRUSKAL DAN DJIKSTRA

3.1 Map

3.2 Graf Kruskal

Keterangan:

1.      Atm BRI di Poltek

2.      Atm BRI di Samping Hotel Damai Indah

3.      Atm BRI di RSIA

4.      Atm BRI di Duta Hotel

5.      Atm BRI di Simpang 4 Kunyit

6.      Atm BRI di Simpang 3 Sarang Halang

7.      Atm BRI di RS Boejasin

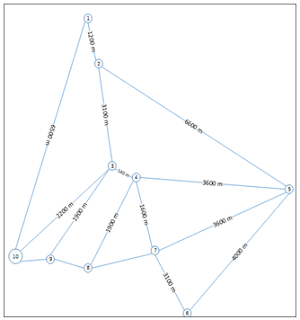
3.3 Graf Djikstra

Keterangan:

0.      Atm BRI di Poltek

1.      Atm BRI di Samping Hotel Damai Indah

2.      Atm BRI di RSIA

3.      Atm BRI di Duta Hotel

4.      Atm BRI di Simpang 4 Kunyit

5.      Atm BRI di Simpang 3 Sarang Halang

6.      Atm BRI di RS Boejasin

7.      Atm BRI di Polres

8.      Atm BRI Pelaihari

9.      Atm BRI Cabang Pelaihari

3.4 Matriks Kruskal

	1	2	3	4	5	6	7	8	9	10
1	0	1200	0	0	0	0	0	0	0	6500
2	1200	0	3100	0	6600	0	0	0	0	0
3	0	3100	0	140	0	0	0	0	1900	2200
4	0	0	140	0	3600	0	1600	1900	0	0
5	0	6600	0	3600	0	4000	3600	0	0	0
6	0	0	0	0	4000	0	3100	0	0	0
7	0	0	0	1600	3600	3100	0	1300	0	0
8	0	0	0	1900	0	0	1300	0	250	0
9	0	0	1900	0	0	0	250	0	0	230
10	6500	0	2200	0	0	0	0	0	220	0

3.5 Matriks Djikstra

	0	1	2	3	4	5	6	7	8	9
0	0	1200	0	0	0	0	0	0	0	6500
1	1200	0	3100	0	6600	0	0	0	0	0
2	0	3100	0	140	0	0	0	0	1900	2200
3	0	0	140	0	3600	0	1600	1900	0	0
4	0	6600	0	3600	0	4000	3600	0	0	0
5	0	0	0	0	4000	0	3100	0	0	0
6	0	0	0	1600	3600	3100	0	1300	0	0
7	0	0	0	1900	0	0	1300	0	250	0
8	0	0	1900	0	0	0	250	0	0	230
9	6500	0	2200	0	0	0	0	0	220	0

3.6 Hasil Running Kruskal

3.7 Hasil Running Djikstra

3.8 Kesimpulan

 Dengan menggunakan algoritma kruskal maupun algoritma djikstra dapat memudahkan seseorang untuk mengetahui jarak terdekat untuk menuju SPBU terdekat dari titik awal lokasi.