HIMPUNAN

PENGERTIAN HIMPUNAN

Himpunan adalah kumpulan benda atau objek yang dapat didefinisikan dengan jelas. Benda atau objek dalam himpunan disebut elemen atau anggota himpunan.

Contoh himpunan:

Himpunan warna lampu lalu lintas, anggota himpunannya adalah merah, kuning dan hijau

Contoh bukan himpunan:

1. Kumpulan baju-baju bagus.

2. Kumpulan makanan enak.

Jenis-jenis Himpunan

Adapun beberapa jenis himpunan yaitu sebagai berikut:

1.   Himpunan Bagian(subset).

2.   Himpunan Kosong.

3.   Himpunan Semesta.

4.   Himpunan Sama (Equal).

5.   Himpunan Lepas.

6.   Himpunan Komplemen.

7.   Himpunan Ekuivalen(equal set).

Penjelasan:

1. Himpunan Bagian(Subset)

Himpunan A dikatakan  himpunan  bagian  (subset)  dari himpunan B ditulis A ⊂ B ”, jika setiap anggota A merupakan anggota dari B.

Syarat :

A ⊂ B, dibaca : A himpunan bagian dari B

A ⊂ B, dibaca : A bukan himpunan bagian dari B

B  ⊂  A dibaca : B bukan himpunan bagian dari A

B  ⊂  A dibaca : B bukan himpunan bagian dari A

Contoh :

Misal   A = { 1,2,3,4,5 } dan B = { 2,4} maka  B ⊂ A

Sebab  setiap  elemen  dalam  B merupakan  elemen  dalam A,  tetapi tidak sebaliknya.

Penjelasan : Dari definisi diatas himpunan bagian harus mempunyai unsur himpunan A  juga merupakan unsur himpunan B.artinya kedua himpunan itu harus saling berkaitan.

         2. Himpunan Kosong(Nullset)

Himpunan kosong adalah himpunan yang tidak mempunyai unsur anggota yang sama sama sekali.

Syarat :

Himpunan kosong = A atau { } Himpunan kosong adalah tunggal

Himpunan kosong merupakan himpunan bagian dari setiap himpunan

Perhatikan : himpunan kosong tidak boleh di nyatakan dengan { 0 }.

Sebab : { 0 } ≠ { }

Penjelasan : dari definisi diatas himpunan kosong adalah himpunan yang tidak mempunyai satupun anggota, dan biasanya himpunan kosong dinotasikan dengan huruf yunani ø (phi).

         3. Himpunan Semesta

Himpunan semesta biasanya dilambangkan dengan “U” atau “S” (Universum) yang berarti himpunan yang memuat semua anggota yang dibicarakan atau kata lainya himpunan dari objek yang sedang dibicarakan.

       4. Himpunan Sama(Equal)

        Bila setiap anggota himpunan A juga merupakan anggota himpunan B, begitu pula sebaliknya.dinotasikan dengan A=BSyarat : Dua buah himpunan anggotanya harus sama.
Contoh :A ={ c,d,e}    B={ c,d,e }   Maka A = BPenjelasan : Himpunan equal atau himpunan sama,memiliki dua buah himpunan yang anggotanya sama misalkan anggota himpunan A {c,d,e} maka himpunan B pun akan memiliki anggota yaitu{c,d,e}.

        5 Himpunan Lepas

Himpunan lepas adalah suatu himpunan yang anggota-anggotanya tidak ada yang sama.

Contoh  C = {1, 3, 5, 7}   dan  D = {2, 4, 6}  Maka himpunan C dan himpunan D saling lepas.

Catatan : Dua himpunan yang tidak kosong dikatakan saling lepas jika kedua himpunan itu tidak mempunyai satu pun anggota yang sama.

        6. Himpunan Komplemen (Complement set)

Himpunan komplemen dapat di nyatakan dengan notasi A^C . Himpunan komplemen jika di misalkan S = {1,2,3,4,5,6,7} dan A = {3,4,5} maka A ⊂ U. Himpunan {1,2,6,7} juga merupakan komplemen, jadi A^C = {1,2,6,7}. Dengan notasi pembentuk himpunan ditulis :

A^C = {x│x Є U, x Є A}

       7. Himpunan Ekuivalen (Equal Set)

Himpunan ekuivalen adalah himpunan yang anggotanya sama banyak dengan himpunan lain.

Syarat : Bilangan cardinal dinyatakan dengan notasi n (A) A≈B, dikatakan sederajat atau ekivalen, jika himpunan A ekivalen dengan himpunan B,

Contoh :

A = { w,x,y,z }→n (A) = 4

B = {  r,s,t,u   } →n  (B) = 4

Maka n (A) =n (B) →A≈B

Penjelasan : himpunan ekivalen mempunyai bilangan cardinal dari himpunan tersebut, bila himpunan A  beranggotakan 4 karakter maka himpunan B pun beranggotakan 4.

Cara Penulisan Himpunan

Ada empat cara untuk menyatakan suatu himpunan, yaitu:

1.   Dengan menyebutkan semua anggotanya (roster) yang diletakkan di dalam sepasang tanda kurung kurawal, dan di antara setiap anggotanya dipisahkan dengan tanda koma. Cara ini disebut juga cara Tabulasi.

Contoh:     A = {a, i, u, e, o}

B = {Senin, Selasa, Rabu, Kamis, Jumat, Sabtu, Minggu}

2.    Menyebutkan syarat anggota-anggotanya, cara ini disebut juga cara deskripsi.

Contoh: ambil bilangan asli kurang dari 5

A = bilangan asli kurang dari 5

3.    Notasi Pembentuk Himpunan : dengan menuliskan ciri-ciri umum atau sifat-sifat umum (role) dari anggotanya.

Contoh Soal :

Nyatakan dengan notasi himpunan dengan menuliskan tiap-tiap anggotanya dan sifat-sifatnya himpunan berikut ini :

A adalah himpunan bilangan asli antara 1 dan 6

Penyelesaian :

A adalah himpunan bilangan asli antara 1 dan 6

Dengan menulis tiap-tiap anggotanya A = {2, 3, 4, 5}

Dengan menulis sifat-sifatnya A = {x | 1 < x <  Asli}Î6, x

4.   Himpunan juga dapat di sajikan secara grafis (Diagram Venn)

Penyajian himpunan dengan diagram Venn ditemukan oleh seorang ahli matematika Inggris bernama John Venn tahun 1881. Himpunan semesta digambarkan dengan segiempat dan himpunan lainnya dengan lingkaran di dalam segiempat tersebut.

Operasi Pada Himpunan

Ada beberapa operasi himpunan, yaitu:

       1. Gabungan

Gabungan (union) dari himpunan A dan B adalah himpunan yang setiap anggotanya merupakan anggota himpunan A atau himpunan B.  Dinotasikan A  B Notasi : A   B = {x | x Є A atau  x Є B}.

      2. Irisan

Irisan (intersection) dari himpunan A dan B adalah himpunan yang setiap anggotanya merupakan anggota dari himpunan A dan anggota himpunan B.

Notasi : A   B = {x | x Є  A dan x Є B}.

       3. Komplemen

Komplemen himpunan A terhadap himpunan semesta S adalah himpunan yang anggotanya merupakan anggota S yang bukan anggota A. Dinotasikan A^c

Notasi : A^c = {x | x Є S dan  x Є A}.

       4. Selisih

Selisih himpunan A dan B adalah himpunan yang anggotanya merupakan anggota himpunan A dan bukan anggota himpunan B. Selisih himpunan A dan B adalah komplemen himpunan B terhadap himpunan A. Dinotasikan A-B

Notasi : A – B = {x | x Є A dan  x Є B}

       5. Hasil Kali Kartesius ( cartesion Product )

Hasil kali kartesius himpunan A dan B, dinotasikan A x B, adalah himpunan yang anggotanya semua pasangan terurut (a,b) dimana a anggota A dan b anggota B

Secara matematis dituliskan : A x B = {(a,b)| a Є A dan b Є B}

Hukum Aljabar Himpunan

  Hukum-hukum pada himpunan dinamakan Hukum –hukum aljabar himpunan.     cukup banyak  hukum yang terdapat pada aljabar himpunan , tetapi disini hanya          dijabarkan  11 saja. Beberapa hukum tersebut mirip dengan hukum aljabar  pada sistem bilangan riil seperti a (b+c) = ab + ac  , yaitu hukum distributif.

Tabel 2. 1 Hukum Aljabar Himpunan

1.   Hukum identitas: A = A A U = A	2.   Hukum null/dominasi: A = A U = U
3.   Hukum komplemen: A  = U A  =	4.   Hukum idempoten: A A = A A A = A
5.   Hukum involusi: = A	6.   Hukum penyerapan (absorpsi): A (A B) = A A (A B) = A
7.   Hukum komutatif: A B = B A A B = B A	8.   Hukum asosiatif: A (B C) = (A B) C A (B C) = (A B) C
9.   Hukum distributif: A (B C) = (A B) (A C) A (B C) = (A B) (A C)	10. Hukum De Morgan: = =
11.  Hukum 0/1 = U = Æ

 Terlihat bahwa hukum- hukum yang berlaku pada himpunan merupakan analogi                     hukum –hukum logika , dengan operator  menggantikan L (dan) , sedangkan operator           menggantikan V ( atau ).

Mengenal Operasi Himpunan

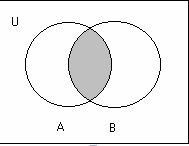
                1. Irisan (Intersection)

              Irisan antara dua buah himpunan dinotasikan oleh tanda ‘∩ ‘.
           Misalkan A dan B adalah himpunan yang tidak saling lepas, maka A ∩ B = { x |            x ∈ A dan x ∈ B }.
          Jika dinyatakan dalam bentuk diagram Venn adalah :

Gambar 2. 1 diagram ven irisan

       Contoh irisan :

       Misalkan A = {2, 3, 5, 7, 11} dan B = {3, 6, 9, 12}, maka A ∩ B = {3}

      2. Gabungan (Union)

Gabungan antara dua buah himpunan dinotasikan oleh tanda‘∪‘. Misalkan A dan B adalah himpunan, maka A ∪ B = { x | x ∈ A atau x ∈ B }

Gambar 2. 2 diagram ven gabungan

Jika dinyatakan dalam bentuk diagram Venn adalah :

Contoh union :

Jika A = { 2, 3, 5, 7} dan B = { 1, 2, 3, 4, 5 }, maka A ∪ B = { 1, 2, 3, 4, 5, 7}

A ∪ ∅ = A

      3. Komplemen (Complement)

Komplemen dari suatu himpunan merupakan unsur -unsur yang ada pada himpunan universal (semesta pembicaraan ) kecuali anggota himpunan tersebut. Misalkan A merupakan himpunan yang berada pada semesta pembicaraan U, maka komplemen dari himpunan A dinotasikan oleh :

Ā = { x | x ∈ U dan x ∉ A }

Jika dinyatakan dalam bentuk diagram Venn adalah :

Gambar 2. 3 diagram ven komplemen

Contoh komplemen :

1.    Misalkan U = { 1, 2, 3, …, 9 },

2.    Jika A = {1, 3, 7, 9}, maka Ā = {2, 4, 5, 6, 8}

3.    Jika A= { x ∈ U | x habis dibagi dua }, maka A= { 1, 3, 5, 7, 9}

Contoh komplemen :

A  =  himpunan mahasiswa STT Telkom

B  =  himpunan mahasiswa yang tinggal di Asrama

C  =  himpunan mahasiswa angkatan 2004

D  =  himpunan mahasiswa yang mengambil matematika diskrit

E = himpunan mahasiswa yang membawa motor untuk pergi ke kampus

a. Pernyataan

“Semua mahasiswa STT Telkom angkatan 2004 yang membawamotor untuk pergi ke kampus” dapat dinyatakan dalam notasi operasi himpunan sebagai berikut :

(A ∩ C) ∩ E

b. Pernyataan

“Semua mahasiswa STT Telkom yang tinggal di asrama dan tidak mengambil matematika diskrit” dapat dinyatakan dalam notasi operasi himpunan sebagai berikut :

A ∩ B ∩ D

c. Pernyataan

“Semua mahasiswa angkatan 2004 yang tidak tinggal di asrama atau tidak membawa motor untuk pergi ke kampus” dapat dinyatakan dalam notasi operasi himpunan sebagai berikut :

C ∩ (B ∪ E)

      4.  Selisih (Dfference)

Selisih antara dua buah himpunan dinotasikan oleh tanda ‘– ‘. Misalkan A dan B adalah himpunan, maka selisih A dan B dinotasikan oleh A – B = { x | x ∈ A dan x ∉ B } = A ∩ B

Gambar 2. 4 diagram ven selisih

                                   

Contoh selisih :

Jika A = { 1, 2, 3, …, 10 } dan B = { 2, 3, 5, 7}, maka A – B = { 1, 4, 6, 8, 9 } dan B – A = ∅

      5.  Beda Setangkup

Beda setangkup antara dua buah himpunan dinotasikan oleh tanda‘⊕‘.
Misalkan A dan B adalah himpunan, maka beda setangkup antara A dan B dinotasikan oleh :

A ⊕ B = (A ∪ B) – (A ∩ B)
= (A – B) ∪ (B – A)

Jika dinyatakan dalam bentuk diagram Venn adalah :

Gambar 2. 5 beda setangkup

Contoh beda setangkup :
Jika A = { 2, 3, 5, 7} dan B = { 1, 2, 3, 4, 5 }, maka A ⊕ B = { 1, 4, 7 }

Beda setangkup memenuhi sifat-sifat berikut :

A ⊕ B = B ⊕ A (hukum komutatif)

(A ⊕ B ) ⊕ C = A ⊕ (B ⊕ C ) (hukum asosiatif)

      6. Perkalian Kartesian

Perkalian kartesian antara dua buah himpunan dinotasikan oleh tanda ‘x’. Misalkan A dan B adalah himpunan, maka perkalian kartesian antara A dan B dinotasikan oleh :

A × B = {(a, b) | a ∈ A dan b ∈ B }

Contoh perkalian kartesian :

Misalkan C = {1, 2, 3}, dan D = { a, b }, maka C × D = { (1, a), (1, b), (2, a), (2, b), (3, a), (3, b) }
Misalkan A = B = himpunan semua bilangan riil, maka A × B = himpunan semua titik di bidang datar

Misalkan ada dua himpunan dengan kardinalitas berhingga, maka kardinalitas himpunan hasil dari suatu perkalian kartesian antara dua himpunan tersebut adalah perkalian antara kardinalitas masing-masing himpunan. Dengan demikian, jika A dan B merupakan himpunan berhingga, maka:

|A × B| = |A| . |B|

Pasangan terurut (a, b) berbeda dengan (b, a), dengan kata lain (a, b) ≠ (b, a). Dengan argumen ini berarti perkalian kartesian tidak komutatif, yaitu:

A × B ≠ B × A

dimana A atau B bukan himpunan kosong. Jika A = ∅ atau B = ∅, maka:

A × B = B × A = ∅

Hukum-hukum yang berlaku untuk operasi himpunan adalah sebagai berikut :

1. Hukum identitas:

a.    A ∪ ∅ = A

b.    A ∩ U = A

2. Hukum null/dominasi:

a.    A ∩ ∅ = ∅

b.    A ∪ U = U

3. Hukum komplemen:

a.   A ∪ A = U

b.   A ∩ A = ∅

4. Hukum idempoten:

a.    A ∪ A = A

b.    A ∩ A = A

5.  Hukum involusi:

6. Hukum penyerapan (absorpsi):

a.    A ∪ (A ∩ B) = A

b.    A ∩ (A ∪ B) = A

7. Hukum komutatif:

a.    A ∪ B = B ∪ A

b.    A ∩ B = B ∩ A

8. Hukum asosiatif:

a.    A ∪ (B ∪ C) = (A ∪ B) ∪ C

b.    A ∩ (B ∩ C) = (A ∩ B) ∩ C

9. Hukum distributif:

a.    A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)

b.    A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

10. Hukum De Morgan:

11. Hukum komplemen:

                  

DAFTAR PUSTAKA

dana, A. (2013, September 02). makalah himpunan dan anggota-anggotanya. Dipetik Agustus 06, 2018, dari makalah himpunan dan anggota-anggotanya: http://anggaradana.blogspot.com

Suryana. (2017, Maret 22). Pengertian himpunan. Dipetik Agustus 06, 2018, dari Pengertian himpunan: http://suryana900.wordpress.com