PENARIKAN KESIMPULAN, ALJABAR BOOLEAN, DAN GERBANG LOGIKA

PENARIKAN KESIMPULAN

Ada beberapa cara dalam penarikan kesimpulan dalam matdis, yaitu:

1. Modus Ponens

2. Modus Tollens

3. Penambahan Dusjungsi

4. Penyederhanaan Konjungsi

5. Silogisme Disjungsi

6. Silogisme Hipotesis

7. Dilema

Penjelasan

1. Modus Ponens

Suatu argumentasi skemanya

Premis 1 : p => q

Premis 2 : p

--------

Kesimpulan : q

Atau bisa juga dinyatakan dalam bentuk [(p => q) Ʌ p] => q.

2. Modus Tollens

Suatu model argumentasi.

Premis 1 : p => q

Premis 2 : ~q

--------

~p
Kesimpulan : ~p

Atau bisa juga dinyatakan dalam bentuk [(p => q) Ʌ ~q] => ~p

3. Silogisme

Suatu model argument yang skemanya:

Premis 1 : p => q

Premis 2 : q => r

----------

Kesimpilan : p => r

Agar lebih ringkas, ketiga prinsip di atas akan di sajikan dalam tabel berikut:

	Ponens	Tollens	Silogisme
Premis 1	p→q	p→q	p→q
Premis 2	p	~q	q→
Kesimpulan	q	~p	p→

Penarikan kesimpulan berdasarkan prinsip modus ponens, modus tollens dan silogisme selalu sah karena merupakan tautologi.

3. PENYEDERHANAAN KONJUNGSI

Jika suatu kalimat dihubungkan dengan "ʌ" maka dapat diambil salah satu komponennya secara khusus.

Contoh dalam kalimat:

p ʌ q : Saya mengambil mata kuliah Logika Matematika dan Kalkulus

Kesimpulan1(p) : Saya mengambil mata kuliah Logika Matematika.

Kesimpulan2(q) : Saya mengambil mata kuliah Kalkulus.

Tabel kebenaran penyederhanaan konjungsi

	Ponens	Tollens	Silogisme
Premis 1	p→q	p→q	p→q
Premis 2	p	~q	q→
Kesimpulan	q	~p	p→

4. SILOGISME DISJUNGSI

Silogisme disjungsi adalah penarikan kesimpulan dimana jika diberikan dua pilihan "p" atau "q" sedangkan "q" tidak dipilih maka kesimpulannya yang dipilih adalah "p".

Contoh kalimat:

p v q : Bulan ini saya akan mudik ke Yogyakarta atau pergi ke Bali.

~q : Bulan ini saya tidak pergi ke Bali.

Kesimpulan(p) : Bulan ini saya mudik ke Yogyakarta.

Tabel kebenaran silogisme disjungsi

5. SILOGISME HIPOTESIS

Silogisme Hipotesis adalah jika diketahui "p → q" dan "q → r" maka kesimpulannya "p → r".

Contoh kalimat:

p : Saya belajar.

q : Saya bisa mengerjakan soal.

r : Saya lulus ujian.

p → q : Jika saya belajar maka saya akan bisa mengerjakan soal.
q → r : Jika saya bisa mengerjakan soal maka saya lulus ujian.
Kesimpulan (p → r) : Jika saya belajar maka saya lulus ujian.

Tabel kebenaran silogisme hipotesis

6. DILEMA

Dilema adalah penarikan kesimpulan jika diketahui "p v q" dan "p → r" dan "q → r" maka kesimpulannya adalah "r".

Contoh kalimat:

p : Hari ini Rizki ulang tahun.

q : Kemarin Bambang juara LKS nasional.

r : Saya akan ditraktir makan bakso.

p v q : Hari ini Rizki ulang tahun dan Kemarin Bambang juara LKS nasional.
p → r : Jika hari ini Rizki ulang tahun maka saya akan ditraktir makan bakso.

q → r : Jika kemarin Bambang juara LKS nasional saya akan ditraktir makan bakso.

Kesimpulan(r) : Saya akan ditraktir makan bakso.

tabel kebenaran dilema

ALJABAR BOOLEAN

Aljabar Boolean atau dalam bahasa Inggris disebut dengan Boolean Algebra adalah matematika yang digunakan untuk menganalisis dan menyederhanakan Gerbang Logika pada Rangkaian-rangkaian Digital Elektronika. Boolean pada dasarnya merupakan Tipe data yang hanya terdiri dari dua nilai yaitu “True” dan “False” atau “Tinggi” dan “Rendah” yang biasanya dilambangkan dengan angka “1” dan “0” pada Gerbang Logika ataupun bahasa pemrograman komputer. Aljabar Boolean ini pertama kali diperkenalkan oleh seorang Matematikawan yang berasal dari Inggris pada tahun 1854. Nama Boolean sendiri diambil dari nama penemunya yaitu George Boole.

Hukum Aljabar Boolean

Dengan menggunakan Hukum Aljabar Boolean ini, kita dapat mengurangi dan menyederhanakan Ekspresi Boolean yang kompleks sehingga dapat mengurangi jumlah Gerbang Logika yang diperlukan dalam sebuah rangkaian Digital Elektronika.

Dibawah ini terdapat 6 tipe Hukum yang berkaitan dengan Hukum Aljabar Boolean

Hukum Komutatif (Commutative Law)

Hukum Komutatif menyatakan bahwa penukaran urutan variabel atau sinyal Input tidak akan berpengaruh terhadap Output Rangkaian Logika.

Contoh :

Perkalian (Gerbang Logika AND)

X.Y = Y.X

Penjumlahan (Gerbang Logika OR)

X+Y = Y+X

Catatan : Pada penjumlahan dan perkalian, kita dapat menukarkan posisi variabel atau dalam hal ini adalah sinyal Input, hasilnya akan tetap sama atau tidak akan mengubah keluarannya.

Hukum Asosiatif (Associative Law)

Hukum Asosiatif menyatakan bahwa urutan operasi logika tidak akan berpengaruh terhadap Output Rangkaian Logika.

Contoh :

Perkalian (Gerbang Logika AND)

W . (X . Y) = (W . X) . Y

Penjumlahan (Gerbang Logika OR)

W + (X + Y) = (W + X) + Y

Catatan : Pada penjumlahan dan perkalian, kita dapat mengelompokan posisi variabel dalam hal ini adalah urutan operasi logikanya, hasilnya akan tetap sama atau tidak akan mengubah keluarannya. Tidak peduli yang mana dihitung terlebih dahulu, hasilnya tetap akan sama. Tanda kurung hanya sekedar untuk mempermudah mengingat yang mana akan dihitung terlebih dahulu.

Hukum Distributif

Hukum Distributif menyatakan bahwa variabel-variabel atau sinyal Input dapat disebarkan tempatnya atau diubah urutan sinyalnya, perubahan tersebut tidak akan mempengaruhi Output Keluarannya.

Hukum AND (AND Law)

Disebut dengan Hukum AND karena pada hukum ini menggunakan Operasi Logika AND atau perkalian. Berikut ini contohnya :

Hukum OR (OR Law)

Hukum OR menggunakn Operasi Logika OR atau Penjumlahan. Berikut ini adalah Contohnya :

Hukum Inversi (Inversion Law)

Hukum Inversi menggunakan Operasi Logika NOT. Hukum Inversi ini menyatakan jika terjadi Inversi ganda (kebalikan 2 kali) maka hasilnya akan kembali ke nilai aslinya.

GERBANG LOGIKA

Gerbang Logika atau dalam bahasa Inggris disebut dengan Logic Gate adalah dasar pembentuk Sistem Elektronika Digital yang berfungsi untuk mengubah satu atau beberapa Input (masukan) menjadi sebuah sinyal Output (Keluaran) Logis. Gerbang Logika beroperasi berdasarkan sistem bilangan biner yaitu bilangan yang hanya memiliki 2 kode simbol yakni 0 dan 1 dengan menggunakan Teori Aljabar Boolean.

Jenis-jenis Gerbang Logika

Terdapat 7 jenis Gerbang Logika Dasar yang membentuk sebuah Sistem Elektronika Digital, yaitu :

Gerbang AND
Gerbang OR
Gerbang NOT
Gerbang NAND
Gerbang NOR
Gerbang X-OR (Exclusive OR)
Gerbang X-NOR (Exlusive NOR)

Penjelasan

Gerbang AND (AND Gate)

Gerbang AND memerlukan 2 atau lebih Masukan (Input) untuk menghasilkan hanya 1 Keluaran (Output). Gerbang AND akan menghasilkan Keluaran (Output) Logika 1 jika semua masukan (Input) bernilai Logika 1 dan akan menghasilkan Keluaran (Output) Logika 0 jika salah satu dari masukan (Input) bernilai Logika 0. Simbol yang menandakan Operasi Gerbang Logika AND adalah tanda titik (“.”) atau tidak memakai tanda sama sekali. Contohnya : Z = X.Y atau Z = XY.

Simbol dan Tabel Kebenaran Gerbang AND (AND Gate)

Gerbang OR (OR Gate)

Gerbang OR memerlukan 2 atau lebih Masukan (Input) untuk menghasilkan hanya 1 Keluaran (Output). Gerbang OR akan menghasilkan Keluaran (Output) 1 jika salah satu dari Masukan (Input) bernilai Logika 1 dan jika ingin menghasilkan Keluaran (Output) Logika 0, maka semua Masukan (Input) harus bernilai Logika 0.

Simbol yang menandakan Operasi Logika OR adalah tanda Plus (“+”). Contohnya : Z = X + Y.

Simbol dan Tabel Kebenaran Gerbang OR (OR Gate)

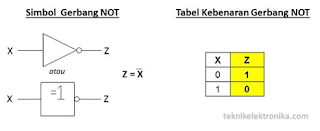
Gerbang NOT (NOT Gate)

Gerbang NOT hanya memerlukan sebuah Masukan (Input) untuk menghasilkan hanya 1 Keluaran (Output). Gerbang NOT disebut juga dengan Inverter (Pembalik) karena menghasilkan Keluaran (Output) yang berlawanan (kebalikan) dengan Masukan atau Inputnya. Berarti jika kita ingin mendapatkan Keluaran (Output) dengan nilai Logika 0 maka Input atau Masukannya harus bernilai Logika 1. Gerbang NOT biasanya dilambangkan dengan simbol minus (“-“) di atas Variabel Inputnya.

Simbol dan Tabel Kebenaran Gerbang NOT (NOT Gate)

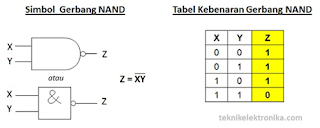
Gerbang NAND (NAND Gate)

Arti NAND adalah NOT AND atau BUKAN AND, Gerbang NAND merupakan kombinasi dari Gerbang AND dan Gerbang NOT yang menghasilkan kebalikan dari Keluaran (Output) Gerbang AND. Gerbang NAND akan menghasilkan Keluaran Logika 0 apabila semua Masukan (Input) pada Logika 1 dan jika terdapat sebuah Input yang bernilai Logika 0 maka akan menghasilkan Keluaran (Output) Logika 1.

Simbol dan Tabel Kebenaran Gerbang NAND (NAND Gate)

Gerbang NOR (NOR Gate)

Arti NOR adalah NOT OR atau BUKAN OR, Gerbang NOR merupakan kombinasi dari Gerbang OR dan Gerbang NOT yang menghasilkan kebalikan dari Keluaran (Output) Gerbang OR. Gerbang NOR akan menghasilkan Keluaran Logika 0 jika salah satu dari Masukan (Input) bernilai Logika 1 dan jika ingin mendapatkan Keluaran Logika 1, maka semua Masukan (Input) harus bernilai Logika 0.

Simbol dan Tabel Kebenaran Gerbang NOR (NOR Gate)

Gerbang X-OR (X-OR Gate)

X-OR adalah singkatan dari Exclusive OR yang terdiri dari 2 Masukan (Input) dan 1 Keluaran (Output) Logika. Gerbang X-OR akan menghasilkan Keluaran (Output) Logika 1 jika semua Masukan-masukannya (Input) mempunyai nilai Logika yang berbeda. Jika nilai Logika Inputnya sama, maka akan memberikan hasil Keluaran Logika 0.

Simbol dan Tabel Kebenaran Gerbang X-OR (X-OR Gate)

Gerbang X-NOR (X-NOR Gate)

Seperti Gerbang X-OR, Gerban X-NOR juga terdiri dari 2 Masukan (Input) dan 1 Keluaran (Output). X-NOR adalah singkatan dari Exclusive NOR dan merupakan kombinasi dari Gerbang X-OR dan Gerbang NOT. Gerbang X-NOR akan menghasilkan Keluaran (Output) Logika 1 jika semua Masukan atau Inputnya bernilai Logika yang sama dan akan menghasilkan Keluaran (Output) Logika 0 jika semua Masukan atau Inputnya bernilai Logika yang berbeda. Hal ini merupakan kebalikan dari Gerbang X-OR (Exclusive OR).

Simbol dan Tabel Kebenaran Gerbang X-NOR (X-NOR Gate)

DAFTAR PUSTAKA

Elektronika, T. (n.d.). Pengertian aljabar boolean hukum aljabar boolean. Retrieved 10 11, 2018, from Pengertian aljabar boolean hukum aljabar boolean: teknikelektronika.com

elektronika, t. (n.d.). Pengertian gerbang logika dasar simbol. Retrieved 10 11, 2018, from Pengertian gerbang logika dasar simbol: teknikelektronika.com

sheemath. (2016, 04). Penarikan Kesimpulan Dalam Logika. Retrieved 10 11, 2018, from Penarikan Kesimpulan Dalam Logika: www.sheemath.com

Cari Blog Ini

Tugas